Recursion: Leave it or Deal with the Negative Consequences
Recursion:
Leave it or Deal with the
Negative Consequences
Jeferson L. R. Souza
thejefecomp@neartword.com
December 31, 2023
Abstract
The moment we acquire knowledge of computer programming—mainly at a professional level—recursion is a technique we definitely avoid to use while either designing or implementing solutions for real-world problems. Although recursion has a great link with Math and a tight relation with heuristics related to Artificial Intelligence (AI), helping defining and understanding a problem in an easy way, the negative consequences of its use may become a nightmare during the execution of an algorithm written with any programming language. In order to avoid the use of recursion, even if we rely on compiler-tools optimisations such as Tail Call Elimination, we should always design an iterative solution from scratch if performance is an intended goal. In this paper-like post, we discuss what recursion is, visiting its drawbacks to understand why we must choose an iterative solution every time we can, being prepared to deal with the negative consequences of recursion if no other option is yet available. We present the example of the Fibonacci’s sequence, where our iterative solution outperforms the recursive one.
Keywords: Computer Programming, Recursion, Performance Botleneck.
1. What is Recursion?
Recursion is a technique used in the design of algorithms, being characterised by the definition of a given function/method that calls itself directly or indirectly in order to solve small parts of the problem in the same way [3, 7]. With its intrinsic repetitive nature, a termination condition must be specified, enabling a recursive algorithm to end the successive function/method calls performed. Upon reaching such a condition, the algorithm starts going backwards, passing through all the previous performed calls until returning a result that represents a solution to the problem being handled. Although it can be straightforward to specify an algorithm using a recursive approach, which is “efficient” in the sense that it is easy to understand at first [6], we should be aware of the negative consequences and the drawback of using recursion when dealing with a considerable workload. We should also be aware of the necessity to address the issue of adapting a given problem to be solved using the computer architecture at hand, mainly while processing a huge volume of data composed by long sequences of inter-dependent and related information.
Performing computer programming activities at professional level gives us both the knowledge and understanding that the use of recursion is only suitable when we are not able to design an iterative algorithm to solve the same problem that an equivalent recursive algorithm is intended to solve. Sedgewick [6, 7] also emphasises the need of removing recursion while implementing an algorithm in a given programming language, as it can be a source of inefficiency to the execution of the software. Some compiler-tools tries to enhance recursive algorithms by providing features such as Tail Call Elimination (TCE) [4, 5].
The TCE feature was designed to improve the performance of a recursive function/method in certain conditions, where the last instruction is a recursive call, converting that last call to a simple iterative loop to prevent the execution penalty of allocating memory for a new function/method call, and other related issues we provide an overview next.
Designing an iterative algorithm from scratch is not exactly the same as using optimisation features provided by compiler tools. Performing such an efficient design is always the best option. Our iterative solution designed from scratch to solve the problem of calculating the value of the nth position of the Fibonacci’s sequence is a vivid and clear example of that. No recursive version is able to beat the iterative algorithm we have designed, which is presented later in this paper-like post.
if we consider the non-usage of compiler-level optimisations, the use of recursion brings a huge limitation on the number of inter-dependent elements we are able to process. The aforementioned limitation is related to the maximum number of recursive calls an operating system can handle while processing a given dataset, i.e., we need to be careful with the limits imposed by the operating system while handling its runtime stack [3, 8, 9].
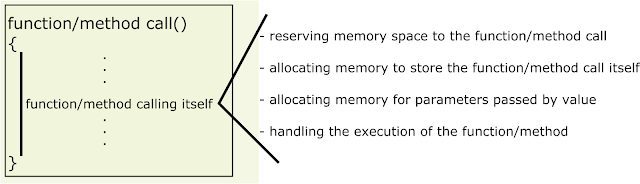
Figure 1 illustrates the hidden details happening when we perform a recursive call of a given function//method. It is important to understand that each recursive call of a given function/method has its own separated memory space, which means that the different calls shares neither internal variables nor local objects/structures, being handled as they are not related at all in respect of its ability to share state [8, 9]. If we would like to share state between distinguished recursive calls, we must do it through setting values of function’s/method’s parameters accordingly.
In order to get a better sense of the drawback the use of recursion may impose in the design of an algorithm, we explain (with more details) in the next section the widely used and known example of calculating the Fibonacci’s sequence numbers using both a recursive and an iterative approaches.
2. Example: The Fibonacci’s Sequence
When speaking about recursion the classic example we are introduced to is the Fibonacci’s sequence. In such a sequence, the value of a given nth position is dependent on its two previous (n − 1)th and (n − 2)th positions, where the base positions (starting with zero) have the predefined value of 1. Therefore, a definition to calculate the nth position of the Fibonacci’s sequence can be specified as follows:
The definition to calculate the Fibonacci’s sequence is straightforward. There is no doubt how to obtain each number of that famous sequence. Next, we present more details about a recursive implementation performed in C language.
2.1 Recursive (naive) Implementation
A recursive algorithm to perform such calculation is extremely similar with the Fibonacci’s recursive definition itself, as illustrated in Algorithm 1. However, the question we must ask here is: Is that simplicity of the algorithm’s specification translated into efficiency when it is executed? Unfortunately, the answer is a “may be”, which depends on the number of elements that need to be handled, the complexity of the solution designed, and the optimisations provider by compiler tools to accelerate the execution of recursive implementations1 .
All recursion trees have almost the same pattern to expand the states from the root to the leaves. However, what differs one tree from another is: (1) the number of subtrees each level is expanded towards; (2) the number of levels; and (3) the combinatory operation that needs to be performed using the elements of each subtree. For the example of the Fibonacci’s sequence, the classical recursive solution—with no improvements to prevent multiple calculations of the same subtree (i.e. states)—generates a recursion tree with two subtrees and two distinguished termination conditions. That classical solution can be represented by the following recurrence, which also indicates how we reach the termination conditions presented in the previous Fibonacci’s definition:
The specified recurrence considers that T(0) = 1, and T(1) = 1, which are the two termination conditions. In addition, the aforementioned recurrence also represents the sum (+) as the combinatory operation performed with the elements of each subtree, which the complexity is constant, i.e., O(1).
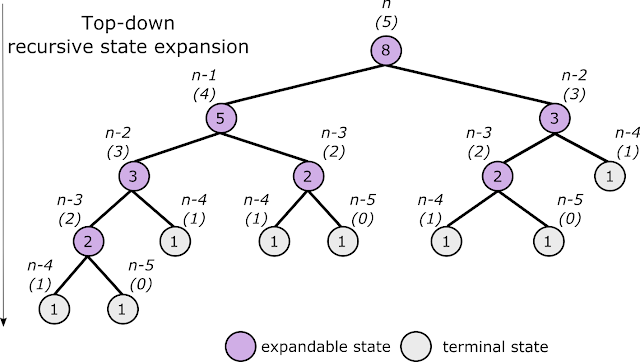
We will not enter in so much details related to the asymptotic analysis of the algorithms presented in this paper-like post. The subject of asymptotic analysis requires a post of its own to be addressed properly. However, just as a matter of providing a better understanding regarding why the classical recursive (naive) implementation of the Fibonacci’s sequence is extremely less efficient than its iterative counterpart, we state that the worst-case execution time of that classical recursive (naive) approach has a complexity of O(2n) if we use a more conservative analysis. It is important to note that the execution-time complexity is tight-related to how a solution is implemented rather than the definition of the problem itself. The high complexity resulting from the presented recursive (naive) implementation is also combined with the high cost of the recursive calls to reach all the states illustrated in the example of Fig. 2; plus the number of combinatory operations that needs to be performed to obtain the intended result.
Figure 2: Graphical representation of the recursion tree illustrating the state expansion for the 5th position of the Fibonacci’s sequence
We known that recursion has been used by a quite some time as a synonym of a computer programming strategy named divide and conquer [2]. However, such an interchangeable usage is far from being true, as we can write an iterative algorithm that uses the divide and conquer strategy in a more efficient way than a recursive one, as described by David Gries in [2].
That confusion about the concepts related to the divide and conquer strategy and recursion have led some misunderstandings when designing efficient algorithms. We do not need to use recursion to apply the divide and conquer strategy, and recursion is (almost) never the better strategy to solve a problem, although, in some specific cases, it achieves a simpler algorithm’s specification that is easier to understand and close to the related problem’s definition.
If we get the Fibonacci’s sequence as an example, we see clearly the simplicity obtained by specifying a recursive algorithm to solve the problem to calculate the nth position of the Fibonacci’s sequence. However, that recursive algorithm does not represent the achievement of an efficient solution. On the contrary, we have a very limited and inefficient one when we want to obtain the value of bigger nth positions present in the Fibonacci’s sequence.
Figure 3: Graphical representation of the recursion tree illustrating the backward calculation for the 5th position of the Fibonacci’s sequence
In the example illustrated by Figs. 2 and 3, some details regarding the execution of its associated recursive (naive) algorithm are revealed. When we analyse the recursion tree of Fig. 2 we observe the duplication of some expandable and terminal states, which are both calculated and reached more than once. The use of such recursive (naive) implementation prevents the self from visualising the summation of the left and right subtrees in a more conscious way, requiring the penalty of computing the same state (e.g., (0),(1),(2), and (3) states) multiple times. The application of the combinatory sum (+) operation on each level is illustrated in Fig. 3, representing the backward execution of the algorithm in order to obtain the result. The bigger the n, the bigger is the number of summations performed backwardly from the terminal states (i.e., the leaves of the recursion tree) towards the expandable (root) state.
In addition, when considering the total number of instructions—i.e., recursive calls plus summations—we need to execute, which are related to the number of states represented by the recursion tree illustrated in Figs. 2 and 3, we are doomed. In the worst-case scenario, where no optimisations are applied, the higher cost of making two new function/method calls for every expandable state is a huge penalty. With compiler optimisations applied, i.e. the TCE feature, although execution perfomance is enhanced, it is still required to compute duplicated states, even if we change a bit the Algorithm 1 to take advantage of a caching strategy achieved through the use of the memoization technique [1].
As a consequence of our analysis of the recursive (naive) implementation presented in Algorithm 1, we achieve the understanding that we are (actually) doing a lot of useless computations. If the reader are not able to reach the same understanding at this point, let us present our iterative (efficient) implementation in order to make such understanding crystal clear.
2.2 Iterative (efficient) Implementation
In the case of the Fibonacci’s sequence, we have washed out all the duplicated states and recursive calls present in the recursive (naive) implementation of Algorithm 1, achieving an extremely efficient worst-case execution time with complexity of O(n), which is obtained through the iterative implementation illustrated in Algorithm 2.
The secret of our extremely efficient implementation is the understanding of the problem we are dealing with, using the minimum effort possible to transform the recursion tree illustrated in both Figs. 2 and 3 into a simple calculated graph that has n+1 states, as illustrated in Fig. 4. It is important to understand that we do not maintain in memory all the states presented in Fig. 4, which are produced during the execution of the software. We just perform a temporary store of the nth calculated position itself plus the required values of both two previous positions (n − 1)th and (n − 2)th to perform the calculation.
Figure 4: Graphical representation of the iterative calculation for the 5th position of the Fibonacci’s sequence
Therefore, the idea behind the Algorithm 2 is extremely simple. Instead of expanding the states recursively and dealing with the negative consequences of performing numerous recursive function/method calls, also handling both calculation and visiting of duplicated states/subtrees, we perform things in a smart way.
Algorithm 2 calculates just once—using an ascending order—a state representing the value of a given position p of the Fibonacci’s sequence, where such calculated state is visited at most twice to perform further calculations when 2 ≤ p ≤ n. Therefore, as the algorithm makes progress towards the nth position, a new state is calculated, storing in memory only the resulting state and the two previous states to perform the calculations. The algorithm stops its execution when the nth position is calculated.
Both algorithms 1 and 2 are present in the small Fibonacci utility program developed by the author, which the source code is available on the following GitHub’s repository: https://github.com/thejefecomp/utilities.
3. Conclusion
In this paper-like post we have presented what recursion is, and why we must choose an iterative solution every time we can, being prepared to deal with the negative consequences of recursion if no other option is yet available. As a vivid example, we have also presented that the iterative (efficient) implementation to address the problem of calculating the nth position of the Fibonacci’s sequence outperforms the recursive (naive) one.
At professional level, where we need to present the better solution possible to the client, choosing an iterative approach is always the better design’s decision, letting the negative consequences of recursion out-of-the-table. How- ever, we need also to be prepared of using recursion in very specific circumstances, being aware of the performance penalty we are introducing in the software being delivered.
Let us design better software with little or no recursion at all.
May the force be with you!
Footnotes
1 Depending on how we have designed a recursive solution, we would perform duplicated recursive calls, which the TCE feature will just eliminate the steps to handle the storage and resume of a function/method call, although the number of internal executed instructions remains almost the same.
References
[1] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to Algorithms, 4th ed., The MIT Press, 2022.
[2] D. Gries, The Science of Programming, Springer-Verlag, 1981.[3] K. R. Irvine, Assembly Language for x86 Processors, 6th ed., Prentice Hall, 2011.
[4] M. Madsen, R. Zarifi, and O. Lhoták, Tail Call Elimination and Data Representation for Functional Languages on the Java Virtual Machine, Proceedings of the 27th International Conference on Compiler Construction, 2018.[5] M. Ralston and D. Mason, Tail Call Elimination in Opensmalltalk, International Workshop on Smalltalk Technologies, 2019.
[6] R. Sedgewick, Algorithms, Addison-Wesley, 1983.
[7] _______ , Algorithms in C, Addison-Wesley, 1990.
[8] A. Silberschatz, P. B. Galvin, and G. Gagne, Operating Systems Concepts, 10th ed., John Wiley & Sons, Inc., 2018.
[9] A. S. Tanenbaum and H. Bos, Modern Operating Systems, 4th ed., Person Education, inc., 2015.